感謝@ tobias-ribizel的使用Neumann series的建議,我安排回答這個問題。如果我們的一部分從下面的公式:
%5E%7B-1%7D*1)
使用紐曼系列:
*1)
如果我們通過矢量我們可以單獨在操作乘以系列每學期矩陣的每一行Q並大致連續地與:
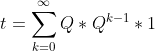
這是Python代碼,我用它來計算這個
def expected_steps_iterative(Q, n=10):
N = Q.shape[0]
acc = np.ones(N)
r_k_1 = np.ones(N)
for k in range(1, n):
r_k = np.zeros(N)
for i in range(N):
for j in range(N):
r_k[i] += r_k_1[j] * Q[i, j]
if np.allclose(acc, acc+r_k, rtol=1e-8):
acc += r_k
break
acc += r_k
r_k_1 = r_k
return acc
這是用放電的代碼。這段代碼預計Q是一個RDD,其中每一行都是一個元組(row_id,該矩陣行的權重字典)。
def expected_steps_spark(sc, Q, n=10):
def dict2np(d, sz):
vec = np.zeros(sz)
for k, v in d.iteritems():
vec[k] = v
return vec
sz = Q.count()
acc = np.ones(sz)
x = {i:1.0 for i in range(sz)}
for k in range(1, n):
bc_x = sc.broadcast(x)
x_old = x
x = Q.map(lambda (u, ol): (u, reduce(lambda s, j: s + bc_x.value[j]*ol[j], ol, 0.0)))
x = x.collectAsMap()
v_old = dict2np(x_old, sz)
v = dict2np(x, sz)
acc += v
if np.allclose(v, v_old, rtol=1e-8):
break
return acc
你看過像GMRES這樣的線性方程組的迭代求解器嗎?他們提供了一些錯誤估計來檢查你需要多少次迭代。 Python在['scipy.sparse.linalg']中提供了它們(https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.gmres。html#scipy.sparse.linalg.gmres) –
對不起,我誤解了你的問題!你看過基本矩陣的[Neumann series representation](https://en.wikipedia.org/wiki/Absorbing_Markov_chain#Fundamental_matrix)嗎?可能僅使用有限數量的力量系列 –
中的加數來近似逆向感謝您的意見@TobiasRibizel。我認爲紐曼系列不是我正在尋找的,因爲它意味着將矩陣乘以幾次。但是,如果我正確理解了GMRES算法,則此解決方案可能以每個組件爲基礎並行化。 –